3DEXPERIENCE
Présentiel | Distanciel
Le flambement est un mode de défaillance critique des structures. Il se produit lorsqu’une structure perd sa capacité de charge sous une charge de compression. La charge de flambement peut être nettement inférieure à la contrainte ultime nécessaire pour provoquer la déformation du matériau. C’est pourquoi il est important d’analyser le flambement dans les structures critiques pour la sécurité. Lorsque le flambement se produit, le chemin d’équilibre primaire, c’est-à-dire le chemin charge-déplacement, subit une bifurcation, comme le montre la figure 1. Au-delà du point de bifurcation se trouve le chemin d’équilibre secondaire où la réponse de la structure peut être hautement non linéaire. C’est le régime de post-flambement.
Les analyses de flambement linéaire peuvent fournir des informations de base sur la charge critique
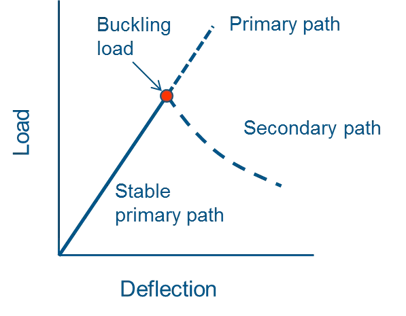
Cependant, la charge d’effondrement de certaines structures est beaucoup plus élevée que la charge de critique prédite par une analyse de flambement linéaire (valeur propre). Dans d’autres cas, une structure retrouvera une partie de sa capacité de charge après avoir flambée. Dans ces deux cas, il est nécessaire d’effectuer une analyse de flambement non linéaire qui inclut le post-flambement.
Une complication qui survient lors de la réalisation d’analyses de flambement non linéaire est que les solveurs statiques généraux qui utilisent la méthode Newton-Raphson ne fournissent pas d’informations sur la réponse post-flambement d’une structure en raison de l’instabilité au point de bifurcation. Ceci est particulièrement préjudiciable lorsque la déformation de la structure produit un relâchement brusque (claquage, ou Snap Through en anglais) où une structure peut avoir plus d’une configuration stable de support de charge. Les fortes accélérations et les effets d’inertie rendent nécessaire l’utilisation d’une procédure dynamique qui tient compte de la masse et de l’inertie de la structure. Nous étudions ici comment la dynamique implicite dans 3DEXPERIENCE peut être utilisée pour modéliser la réponse non linéaire au flambement et au post-flambement d’une structure.
Un panneau de fuselage d'avion est un exemple de structure pouvant subir un flambement
Ces panneaux sont constitués d’une peau mince renforcée par des longerons dans le sens longitudinal pour améliorer leur capacité de charge. Des cadres peuvent également être ajoutés pour améliorer la rigidité dans la direction circonférentielle, mais ils ne seront pas pris en compte dans cette analyse pour des raisons de simplicité. Le panneau étudié est représenté sur la figure 2.
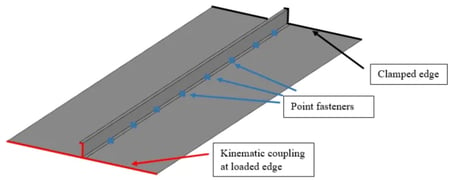
figure 2
Le panneau est constitué d’une fine peau rectangulaire d’une épaisseur de 2 mm, d’une longueur de 600 mm et d’une largeur de 220 mm. La peau est renforcée par un longeron en Z d’une épaisseur de 1,6 mm, d’une hauteur d’âme de 25 mm et d’une largeur d’aile de 20 mm. Comme les épaisseurs de la peau et du longeron sont très faibles par rapport à leurs autres dimensions, la structure est modélisée à l’aide d’éléments de coque S8R (Shell 8 Nodes, Reduced Integration). De l’aluminium (E = 70 GPa, ν= 0,3) avec un comportement de matériau élasto-plastique est utilisé pour les deux pièces. Le longeron est fixé à la peau à l’aide de points de soudures et un couplage cinématique est défini à un bord du panneau de sorte que les bords de la peau et du longeron soient couplés à un point de référence. Ce point de référence sera utilisé pour introduire des charges de force et de déplacement. Le bord opposé du panneau est entièrement fixé. Tout d’abord, une analyse de flambement linéaire est effectuée avec une charge de compression de 20 kN appliquée au point de référence sur le bord chargé. Les résultats indiquent que la charge de flambement de la peau est d’environ 18 kN. La forme déformée du panneau est illustrée à la figure 3.
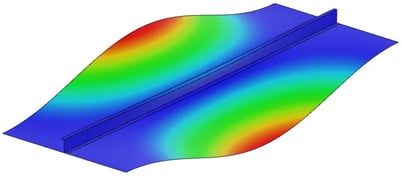
figure 3
Pour les panneaux renforcés, la charge de flambement de la peau est généralement beaucoup plus faible que la charge d'effondrement de la structure entière
Par conséquent, il est nécessaire d’effectuer une analyse de flambement non linéaire complète qui inclut le post-flambement. Dans des simulations plus complexes, une imperfection géométrique basée sur les premiers modes de flambement pourrait être introduite dans la géométrie avant l’analyse de post-flambement. On peut également introduire une imperfection de chargement. Il est bien connu que les structures « imparfaites » ont des charges de flambement beaucoup plus faibles que les structures « parfaites ». Cependant, pour la présente analyse, une imperfection n’est pas introduite, car le but est de démontrer la robustesse du solveur de dynamique implicite.
À titre de comparaison, l’analyse est également effectuée à l’aide d’une procédure statique avec stabilisation pour réduire les effets d’inertie. Dans l’analyse statique, une charge de compression de 100 kN est appliquée au bord chargé. La courbe charge-déplacement obtenue est illustrée à la figure 4. Nous pouvons voir que la peau se déforme à une charge de 17,68 kN, comme l’indique le léger point d’inflexion dans la réponse, mais la structure s’effondre à une charge beaucoup plus élevée, c’est-à-dire environ 74 kN. La figure 5 montre la forme déformée du panneau et le contour de l’amplitude du déplacement.
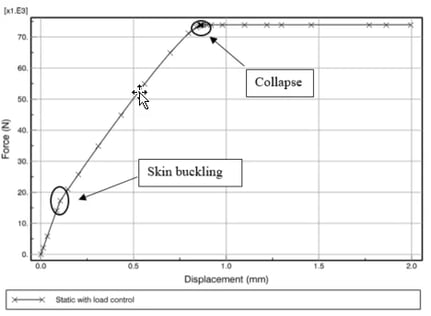
figure 4
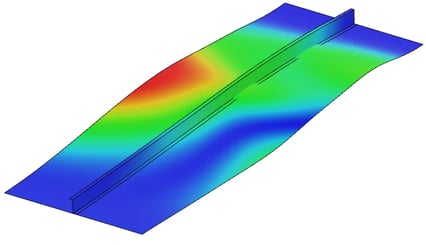
figure 5
La procédure statique ne parvient pas à fournir une solution au-delà d'un déplacement de 2,0 mm
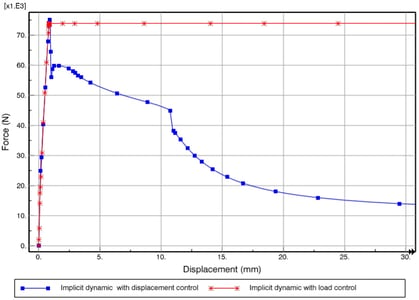
figure 6
Par conséquent, nous allons effectuer une analyse de flambement non linéaire en utilisant la dynamique implicite avec un contrôle de la charge et un contrôle du déplacement. Pour le cas contrôlé par la charge, nous appliquons une charge de compression de 100 kN au point de référence sur le bord chargé (comme pour les analyses statiques et des valeurs propres). Pour le cas où le déplacement est contrôlé, nous appliquons un déplacement en compression de 150 mm au point de référence. Les réponses force-déplacement des deux cas sont présentées sur la figure 6.
En utilisant la dynamique implicite, nous pouvons voir qu’une solution post-flexion peut facilement être obtenue. Dans ce cas, le solveur n’a aucun problème à produire une solution au-delà de la charge d’effondrement des structures puisque nous prenons en compte la masse (inertie) du panneau et l’utilisons pour résoudre les équations complètes du mouvement dans le domaine temporel. Par conséquent, le panneau est capable de supporter une déformation bien au-delà de la charge d’effondrement. Le cas contrôlé par la charge a été interrompu manuellement après que le déplacement du panneau ait atteint 150 mm et le cas contrôlé par le déplacement a fourni avec succès une solution jusqu’à 150 mm.
Cependant, nous pouvons constater que le panneau ne retrouve aucune de ses rigidités structurelles dans le régime de post-flexion. Il s’agit d’un outil particulièrement utile pour les problèmes de flambement de type « snap-through », où une structure peut avoir une certaine rigidité au-delà du point de flambement. Dans ce cas, nous pouvons voir que le panneau continue à se déformer sans aucune augmentation de la charge. La forme finale du flambement est illustrée à la figure 7 et les contours de déplacement sont illustrés à la figure 8.
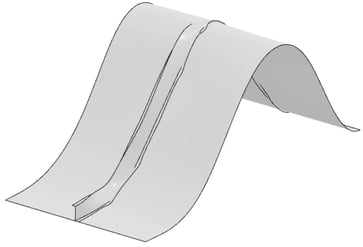
figure 7
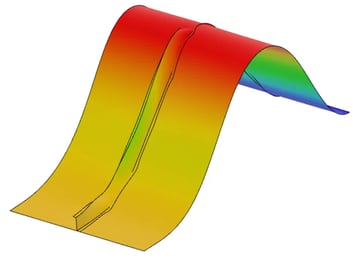
figure 8
Source blog SOLIDWORKS Dassault Systèmes
Nos ressources
Découvrez d'autres articles de blog
FD03 : La conception à portée de clic
Gagnez en productivité et en créativité avec 3DEXPERIENCE SOLIDWORKS FD03. Des outils puissants pour une conception ...
Découvrir
DraftSight : Une alternative incontournable aux logiciels CAO 2D
Depuis sa création en 2010, DraftSight s'est imposé comme une alternative incontournable aux logiciels de CAO 2D ...
Découvrir
Eco conception : Quels sont les enjeux ?
La plateforme 3DEXPERIENCE offre une solution complète pour intégrer l'éco-conception dans vos processus de ...
Découvrir
VOUS SOUHAITEZ PLUS DE RENSEIGNEMENTS SUR ABAQUS SIMULATION ?
Nos spécialistes Dassault Systèmes de Abaqus sont à votre écoute pour planifier votre rendez-vous et vous aiguiller sur les solutions les plus appropriées à vos projets.
